Iepriekšējā nodarbībā mēs aplūkojām plusus un mīnusus izlaušanās spēlēm, kas veidotas pēc atvērtā ceļa principa. Šajā nodarbībā iepazīstināsim jūs ar trešo un pēdējo spēles struktūras veidu, ko aprakstījis Nikolsons (2015): multilineāro ceļu.
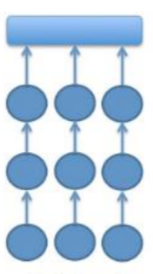
Daudzlīniju struktūru, ko Nikolsons (2015) dēvēja par “uz ceļiem bāzētu” (“path-based”) secību, var aprakstīt kā sajaukumu starp lineāro un atvērto ceļu. Iesākumā vienlaikus jāatrisina vairāki lineārie ceļi. Pie katra no tiem var strādāt mazas grupas vai individuāli skolēni. Pēc tam, līdzīgi kā atvērtajā ceļā, ir jāatrisina meta-mīkla, izmantojot atbildes, norādes un citus risinājumus, kas iegūti no katra lineārā ceļa pēdējās mīklas. Šeit ir paskaidrojoša diagramma no Nikolsona raksta:
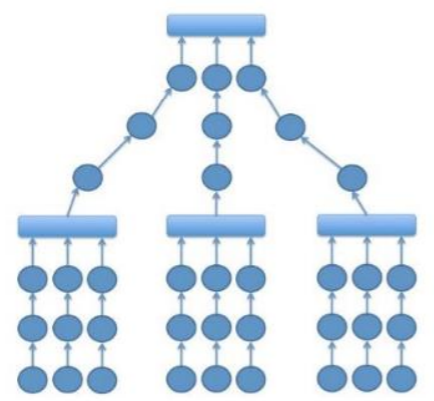
Savā darbā Nikolsons (2015) apspriež arī hibrīdu modeļus, kas apvieno lineāros, atvērtos un multilineāros ceļus, sevišķi izceļot to, ko viņš sauc par piramīdu. Zemāk redzamā ilustrācija piedāvā labāku piramīdas ceļa koncepcijas vizuālu skaidrojumu.
Pamatojoties uz Nikolsona atzinumiem, savā sekojošajā rakstā Wiemker et al. (2015) pauž citādu viedokli. Viņi uzskata, ka daudzlīniju struktūras iekļauj abas secības, kuras Nikolsons sauc par “uz ceļa balstītām” un “hibrīdām” struktūrām. Tāpēc, pēc viņu domām, multilineārie ceļi sevī ietver visas sarežģītās struktūras.
Pamatojoties uz iepriekš minēto, daudzlīniju ceļi var krustoties, un tiem ir dažādi beigu punkti. Mīklas visas var būt pieejamas jau no paša sākuma, vai arī tās var atklāt spēles gaitā. Tos var ietvert citās mīklās, ievērojot Matrjoškas modeli (piemēram, slēgta kaste slēgtas lādes iekšpusē).
Ilustrācija
Šī infografika no Wiemker et al. (2015) varētu palīdzēt jums vizualizēt, ko mēs domājam ar multilineāro jeb daudzlīniju ceļu.
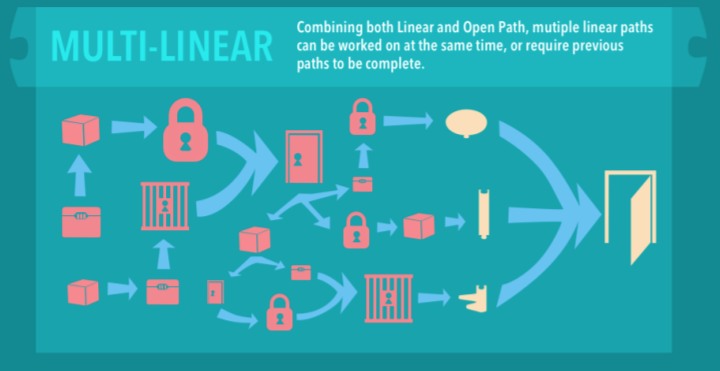
No sākuma mums ir divi dažādi uzdevumi: kaste un lāde, kas jāatver (norādītas infografika kreisajā pusē). Katrs no tiem pieder pie atsevišķiem lineāriem ceļiem, kas ved uz pirmo meta-mīklu – durvīm (infografikas augšējā centrālā daļā). Šīs meta-mīklas atrisināšana atklāj trīs jaunus atsevišķus lineāros ceļus (infografikas centrā). Katra ceļa pēdējā mīkla dod spēlētājiem atslēgas daļas (dzeltenā krāsā), kuras jāapvieno, lai atvērtu izejas durvis.
Kad esam izskaidrojuši, kā var izveidot multilineāro ceļu, apskatīsim šīs uzdevumu struktūras plusus un mīnusus.
Plusi
Sāksim ar to, ka daudzlīniju ceļi ir visizplatītākie visā pasaulē. Nikolsons (2015) tos atrada 45% no 175 apsekotajiem objektiem. Šim ceļam ir daudz priekšrocību izglītojošu glābšanās telpu kontekstā. Pirmkārt, līdzīgi kā lineāriem ceļiem, tam ir / var būt skaidri sākuma un beigu punkti. Otrkārt, līdzīgi kā atvērtā ceļa gadījumā, līdz pat desmit skolēniem var vienlaicīgi strādāt pie kādas no mīklām, būdami sadalīti mazās komandās.
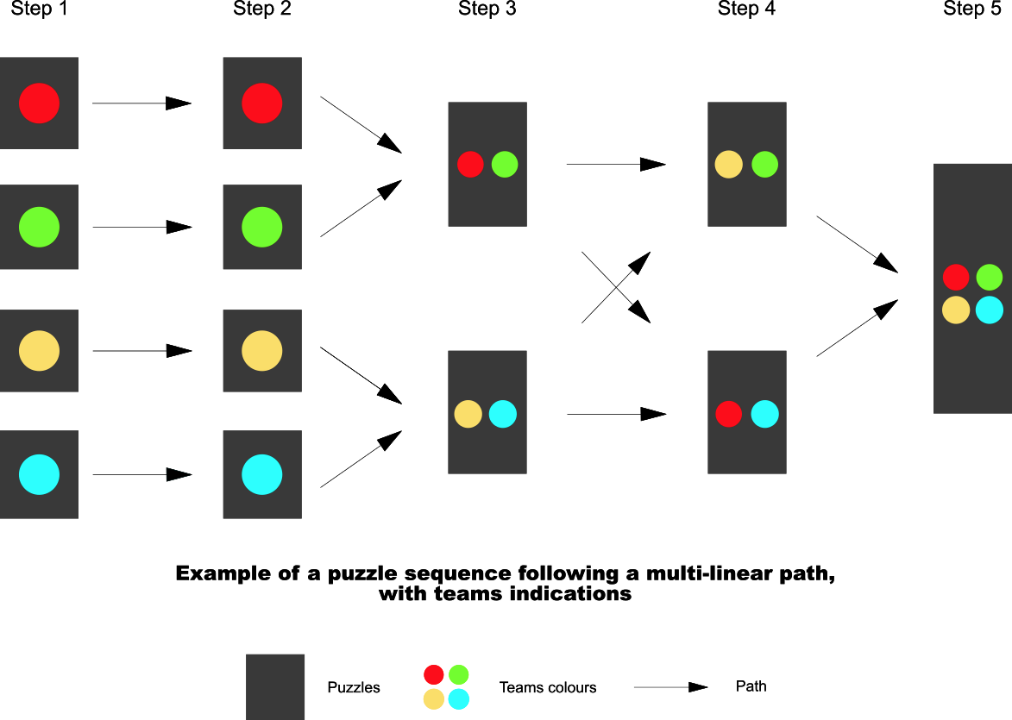
Lai to izdarītu, jūs varētu, piemēram, ieviest krāsu kodu, kas atbilst gan mīklām, gan skolēnu komandām. Katrai komandai tiks piešķirta krāsa, un tai būs jāstrādā pie konkrēti ar šo krāsu saistītajiem uzdevumiem. Meta-mīklas, kurām nepieciešama vairāku komandu sadarbība, varētu apzīmēt ar etiķeti ar vairāku komandu krāsām. Zemāk jūs kā piemēru atradīsiet uzdevumu secību, kas pa posmiem ir sadalīta uz komandām. Mīklu secības iespējas ir bezgalīgas.
Tomēr krāsu kodam nevajadzētu atturēt studentus palīdzēt viens otram starp komandām. Tāpēc jums sākumā skaidri jāinformē skolēni, ka viņiem ir ne tikai atļauts, bet pat ieteicams palīdzēt viens otram gūt panākumus dotajā laika posmā.
No visām piedāvātajām secībām daudzlīniju ceļi visvairāk liek dalībniekiem izmantot sadarbību. Lai gūtu panākumus šajā ceļā, dalībniekiem jāapspriež savi atklājumi un risinājumi, kā arī visas problēmas vai grūtības, ar ko viņi saskaras.
Multilineārais ceļš būs piemērots lielākajai daļai skolēnu, ja izveidosiet to ar skaidrām instrukcijām un pielāgojamu grūtības pakāpi.
Mīnusi
Daudzlīniju ceļu galvenais trūkums ir to sarežģītība projektēšanā un būvēšanā. Būs nepieciešamas vairākas testu un pielāgojumu kārtas, lai no spēles izslēgtu visus traucējumus un kļūdas. Jūs nevarat cerēt, ka iegūsiet perfektu rezultātu jau no pirmā mēģinājuma, it īpaši istabas radīšanas procesa sākumā. Panākumu atslēga šeit būs neatlaidība.
Šādu spēles struktūru radīšana prasīs arī vairāk laika nekā atvērtie un lineārie ceļi, jo būs jāuzstāda vairāki uzdevumi un mīklas.
Vēl jāpiebilst, ka iesācēji un jauni skolēni šādā spēlē var justies apmaldījušies un apmulsuši. Kā minēts iepriekš, šo problēmu var atrisināt, izmantojot krāsu kodu, lai virzītu komandas uz mīklām, kas būs jārisina konkrēti viņiem. Taču arī ar saprotamu skaidrojumu spēles sākumā kopā ar mājieniem nepieciešamības gadījumā šo problēmu var novērst tikpat labi.
Lietas, kas jāpatur prātā, veidojot mīklu secības struktūru
Formulējot un veidojot jebkuru no trīs mīklu secībām, ko aplūkojām 13.-15. nodaļā, paturiet prātā sekojošus punktus:
- Jums var rasties vilinājums izveidot lielu skaitu uzdevumu. Centieties no tā izvairīties, paturot prātā, cik laika atvēlēts visai izlaušanās spēlei. Tas palīdzēs ietaupīt jūsu laiku. Pareizais mīklu skaits vienā secībā būs atkarīgs no jūsu klases, skolēnu vecuma un grūtības pakāpes, kurai jābūt mainīgai. Tāpēc labākais risinājums ir eksperimentēt.
- Norādiet skaidrus sākuma un beigu punktus, lai skolēni nezaudētu pārāk daudz laika, nesaprašanā klaiņojot pa istabu.
- Lai noturētu skolēnu uzmanību un sniegtu tiem pastāvīgu gandarījuma sajūtu, jūs varat ļaut viņiem sasniegt daudz mazu uzvaru visas spēles garumā (Escape rooms on social entrepreneurship, 2019) – piemēram, atrast apslēptu pogu, kas atvērs durvis, aiz kurām būs paslēpts papildu mājiens par to, kā izmantot sākotnēji saņemto norādi par mīklas atrisinājumu.
- Lai process būtu organizēts, izveidojiet savas mīklu struktūras shēmu, it īpaši, ja plānojat veidot daudzlīniju ceļu. Zemāk jūs redzēsiet shēmas piemēru. Lai gan šajā piemērā, iespējams, ietverts pārmērīgs daudzums mīklu, tas labi parāda nepieciešamību vizualizēt savas spēles struktūru, ja esat izlēmis izveidot sarežģītu ceļu.
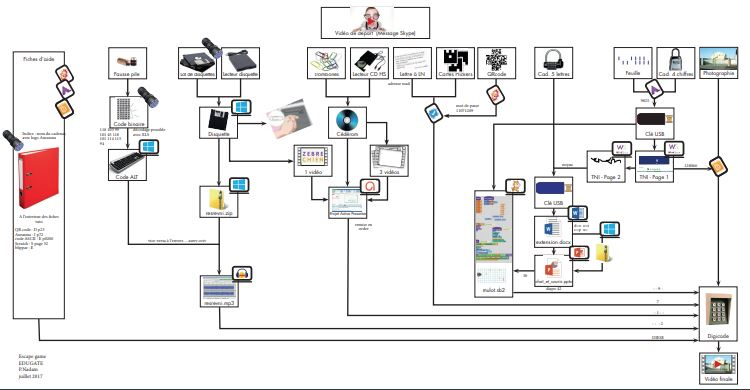
Multilineārais ceļš bija pēdējā no struktūrām, ko aprakstījis Nikolsons (2015). Tagad jums ir visas nepieciešamās zināšanas, lai izveidotu savu ideālo mīklu secību. Nākamā nodarbība sniegs jums tiešsaistes rīkus, lai turpinātu izlaušanās istabas izveidi.