In the previous lesson, we have been over the pros and cons of creating puzzles following an open path for your escape rooms. In this lesson, we will introduce the third and last path described by Nicholson (2015): the multi-linear path.
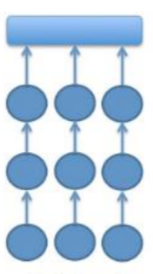
The multi-linear structure – named ‘path-based’ by Nicholson (2015) – can be described as a mix of the linear and open paths. First, a collection of linear paths must be solved simultaneously. Small groups or individuals can work on each path. The second step is, similarly to the open path, a meta-puzzle, which should be solved using the answers, clues and other solutions given after the last puzzles of each of the linear paths. Here is an explicative diagram from Nicholson’s article.
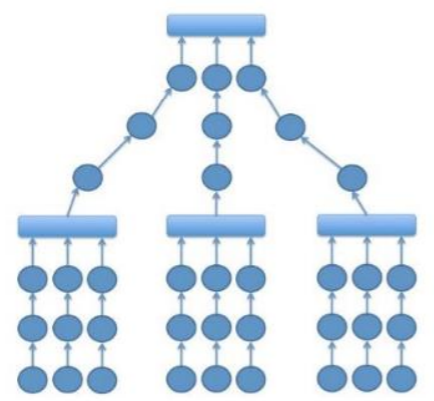
In his work, Nicholson (2015) also discusses hybrid models, mixing linear, open, and multi-linear paths. He highlights one that he calls ‘pyramid’. The illustration below offers a better visual explanation of the pyramid path concept.
In their subsequent article, based on Nicholson’s review, Wiemker et al. (2015) adopt a different view. They consider multi-linear structures as including both of which Nicholson calls ‘path-based’ and ‘hybrid’ structures. Therefore, according to them, multi-linear paths are inclusive of all complex structures.
Based on the above, multi-linear paths can intersect and have varying ending points. Puzzles can all be available from the start or can be revealed as the game goes on. They can be contained within other puzzles, following a Matryoshka / Russian doll pattern (e.g. a closed box inside a closed chest).
Illustration
The following infographic from Wiemker et al. (2015) might help you visualise what we mean by ‘multi-linear path’.
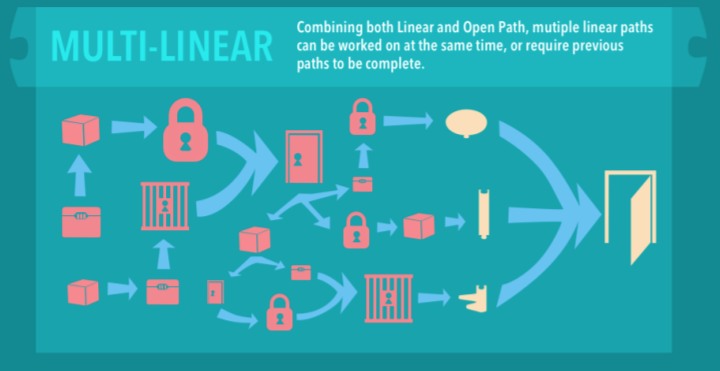
From the start, we have two different puzzles: a box and a chest (indicated on the left-hand side of the infographic). Each belongs to separate linear paths, which lead to a first meta-puzzle, the door (upper centre section of the infographic). Solving this meta-puzzle uncovers three new individual linear paths (centre of the infographic). The last puzzle of each path gives the players parts of a key (in yellow), which are to be combined for the exit door to open.
After having explained how a multi-linear path can be formulated, let’s examine the pros and cons of this puzzle path structure.
Pros
To begin with, multi-linear paths are the most widespread around the world. Nicholson (2015) found it in 45% of the 175 surveyed facilities. This path has many advantages in the context of educative escape rooms. First, similarly to linear paths, it has / can have clear starting and ending points. Second, similarly to the open path, up to ten students – divided into small teams – can work on its puzzles at the same time
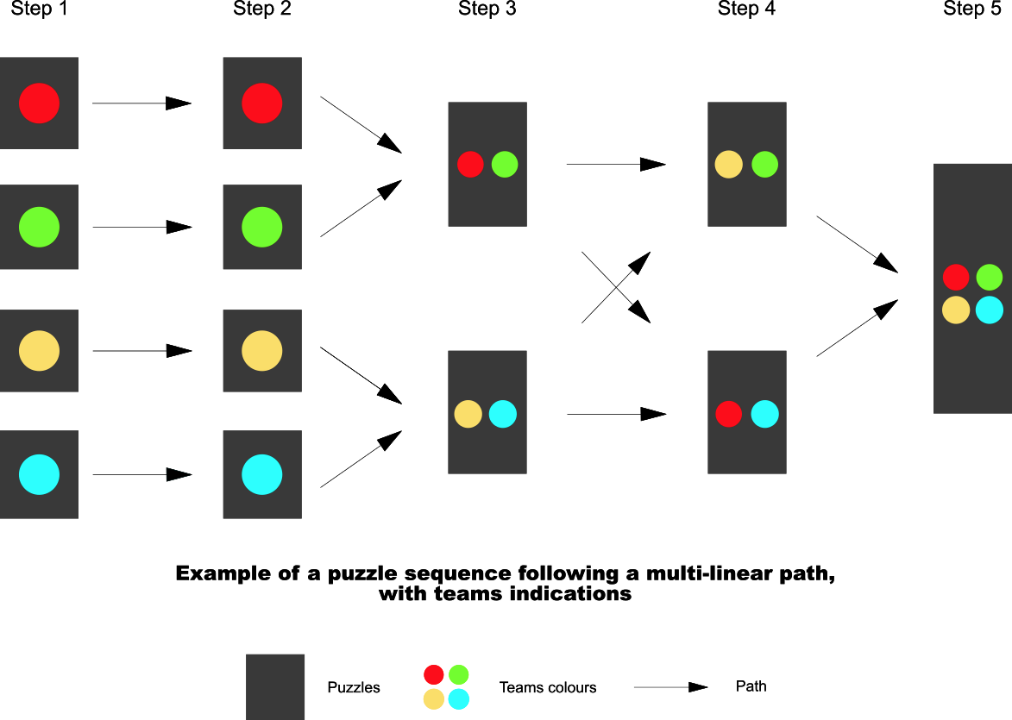
To do so, you could consider applying a colour code to both your puzzles and your students’ teams. Each team would be given a colour and would have to work on a specific set of puzzles linked to the colour. Meta-puzzles – which require the collaboration of several teams – could be indicated by a label with several team colours. You will find an example of a puzzle sequence divided into teams below. Possibilities of puzzle sequences are infinite.
However, the colour code should not refrain students from helping each other between teams. Therefore, you should express clearly at the beginning that they will have the right – and should – help each other, to succeed in the given time frame.
Of all sequences, multi-linear paths foster collaboration and cooperation the most. With this path, students will have to discuss their discoveries and solutions, as well as problems and difficulties, in order to succeed.
With clear instructions and different levels of difficulty, the multi-linear path will suit most of your students.
Cons
On the contrary, multi-linear paths’ main disadvantage is their complexity to design and to build. Several phases of test and adjustments will be necessary to eliminate all glitches and mistakes from the sequence. You cannot expect to get it right from the first try, especially at the beginning of your creation process. Perseverance will be the key!
Complementarily, their creation will be more time consuming than with open and linear paths, as more puzzles must be set up.
Lastly, beginner and young students might find themselves lost and confused. As mentioned above, this problem can be solved by using a colour code, to direct teams towards the enigma they will need to address. Alternatively, a clear explanation, in the beginning, coupled with hints in case of need, will do the job as nicely.
Points to keep in mind when structuring your puzzle sequence
When formulating any of the three puzzle sequences analysed throughout lessons 13 to 15, there are some points you should keep in mind:
- It might be tempting to create a lot of puzzles. Try to avoid this by keeping in mind the time allowed to solve the room. It will save you time. The right number of puzzles per sequence will depend on your class, your students’ age, and the level of difficulty, which should be variable. Therefore, the best solution is to experiment.
- Make sure to indicate clear starting and ending points, to avoid losing too much time with confusion and wandering around the room.
- You can distribute small successes along the way, to keep students’ attention and give them an ongoing sense of accomplishment (Escape rooms on social entrepreneurship, 2019) – like finding a clue or a hidden button that will open a door which will give a further hint on how to use the initial clue to solve the puzzle.
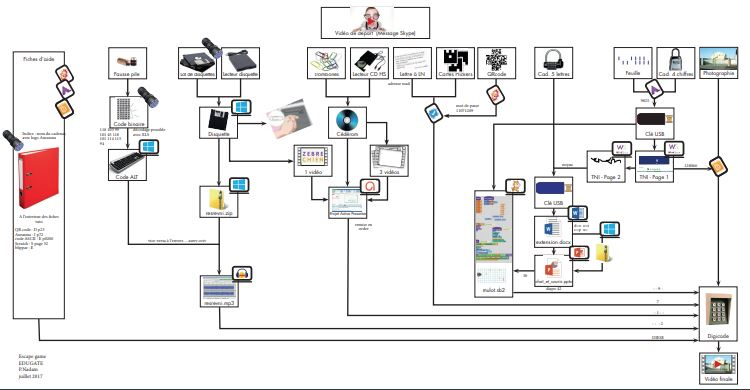
- Create a scheme of your puzzle structure, especially if you engage in a multi-linear path, to organise yourself. You will find a mapped example below. Although it might be slightly excessive, as the number of puzzles is important, it illustrates well the necessity to map your structure if you decide to create a complex path.
To conclude, the multi-linear path was the last structure observed by Nicholson (2015). You now hold all the cards to create the perfect puzzle sequence. The next grain will give you online tools to proceed with Escape room creation.