Στο προηγούμενο μάθημα, αναφερθήκαμε στα πλεονεκτήματα και τα μειονεκτήματα της δημιουργίας παζλ για τα δωμάτια διαφυγής σας, τα οποία ακολουθούν μια ανοιχτή διαδρομή. Σε αυτό το μάθημα, θα παρουσιάσουμε την τρίτη διαδρομή που περιγράφεται από τον Nicholson (2015): την πολυγραμμική διαδρομή.
Η πολυγραμμική δομή – που ονομάζεται «βασική διαδρομή» από τον Nicholson (2015) – μπορεί να περιγραφεί ως ένα μείγμα γραμμικών και ανοιχτών διαδρομών. Πρώτον, ένα σύνολο γραμμικών διαδρομών πρέπει να λυθεί ταυτόχρονα. Μικρές ομάδες ή μεμονωμένα άτομα μπορούν να δουλέψουν πάνω σε κάθε διαδρομή. Το δεύτερο βήμα, παρόμοιο με την ανοιχτή διαδρομή, είναι ένα μεταπάζλ, το οποίο πρέπει να λυθεί με βάση τις απαντήσεις, τα στοιχεία, και άλλες λύσεις που δόθηκαν στα προηγούμενα παζλ κάθε γραμμικής διαδρομής. Ακολουθεί ένα επεξηγηματικό διάγραμμα από το άρθρο του Nicholson.
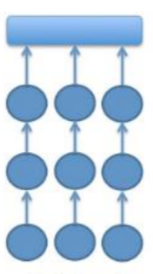
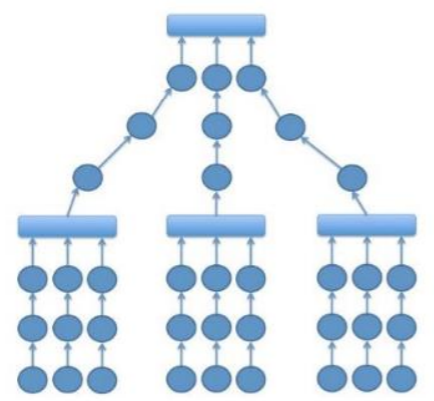
Στο έργο του, ο Nicholson (2015) αναφέρει επίσης τα υβριδικά μοντέλα, ένας συνδυασμός γραμμικών, ανοιχτών και πολυγραμμικών διαδρομών. Αυτόν τον συνδυασμό αποκαλεί «πυραμίδα». Η παρακάτω εικόνα παρέχει μια καλύτερη οπτική επεξήγηση για τη διαδρομή της πυραμίδας.
Στο επόμενο άρθρο τους, με βάση την αξιολόγηση του Nicholson, οι Wiemker et al. (2015) υιοθετούν μια διαφορετική άποψη. Θεωρούν πολυγραμμικές δομές αυτές που ο Nicholson αποκαλεί «βασική διαδρομή» και «υβριδική» δομή. Επομένως, σύμφωνα με τη δική τους άποψη, οι πολυγραμμικές διαδρομές περιλαμβάνουν όλες τις πολύπλοκες δομές.
Με βάση τα παραπάνω, οι πολυγραμμικές διαδρομές μπορούν να τέμνονται και να έχουν διαφορετικά σημεία κατάληξης. Τα παζλ μπορούν να είναι όλα διαθέσιμα από την αρχή ή μπορούν να αποκαλυφθούν καθώς το παιχνίδι εξελίσσεται. Μπορούν να ενσωματωθούν σε άλλα παζλ, ακολουθώντας το μοτίβο της κούκλας Ματριόσκα/Μπαμπούσκα (π.χ. ένα κλειστό κουτί μέσα σε ένα κλειστό σεντούκι).
Εικόνα
Το ακόλουθο ενημερωτικό γράφημα από τον Wiemker et al. (2015) μπορεί να σας βοηθήσει να σχηματίσετε μία εικόνα για το τι σημαίνει η πολυγραμμική διαδρομή.
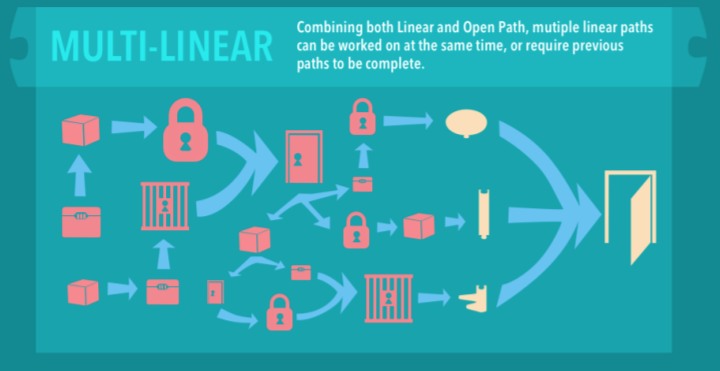
Από την αρχή, έχουμε δύο διαφορετικά παζλ: ένα κουτί και ένα σεντούκι (υποδεικνύεται στην αριστερή πλευρά του ενημερωτικού γραφήματος). Το καθένα ανήκει σε ξεχωριστές γραμμικές διαδρομές, οι οποίες οδηγούν σε ένα πρώτο μεταπάζλ, την πόρτα (πάνω στο κέντρο του ενημερωτικού γραφήματος). Η επίλυση αυτού του μεταπάζλ αποκαλύπτει τρεις νέες μεμονωμένες γραμμικές διαδρομές (στο κέντρο του ενημερωτικού γραφήματος). Το τελευταίο παζλ κάθε διαδρομής δίνει στους παίκτες τα μέρη ενός κλειδιού (με κίτρινο χρώμα), τα οποία πρέπει να συνδυαστούν για να ανοίξει η πόρτα εξόδου.
Αφού εξηγήσαμε πώς μπορεί να διαμορφωθεί μια πολυγραμμική διαδρομή, ας εξετάσουμε τα πλεονεκτήματα και τα μειονεκτήματα αυτής της διαδρομής.
Πλεονεκτήματα
Κατ’ αρχάς, οι πολυγραμμικές διαδρομές είναι οι πιο διαδεδομένες σε όλο τον κόσμο. Ο Nicholson (2015) βρήκε τη συγκεκριμένη διαδρομή στο 45% των 175 εγκαταστάσεων που ερεύνησε. Αυτή η διαδρομή έχει πολλά πλεονεκτήματα στο πλαίσιο των εκπαιδευτικών δωματίων διαφυγής. Πρώτον, έχει / μπορεί να έχει σαφή σημεία έναρξης και λήξης όπως οι γραμμικές διαδρομές. Δεύτερον, στην πολυγραμμική διαδρομή μπορούν να εργαστούν ταυτόχρονα στα παζλ έως και δέκα μαθητές – χωρισμένοι σε μικρές ομάδες – σας και στην ανοιχτή διαδρομή.
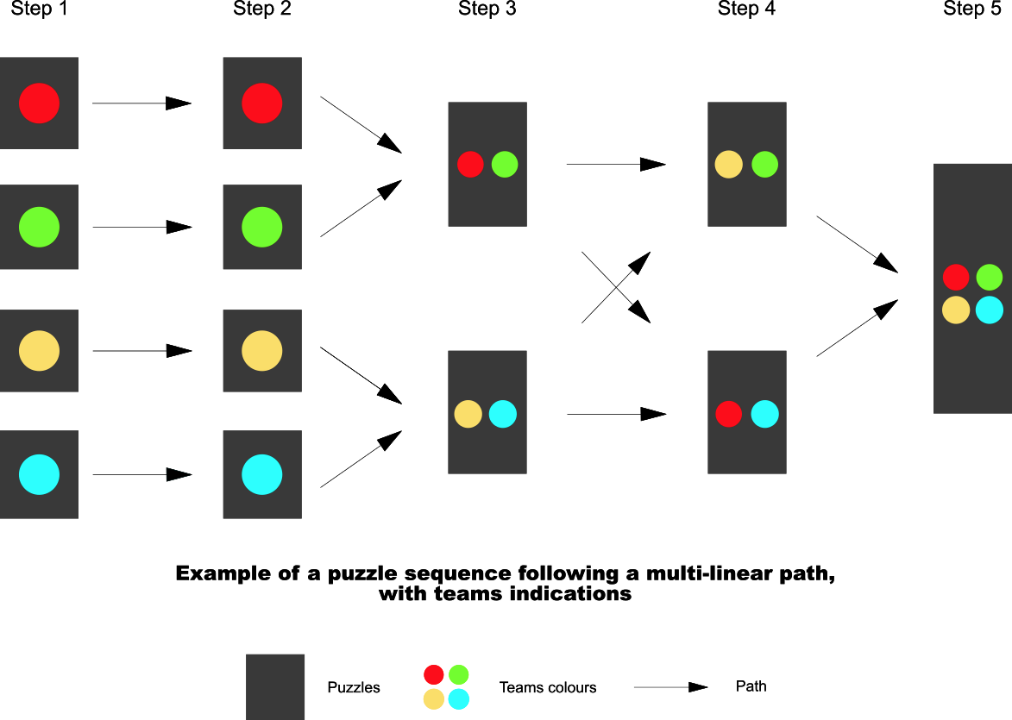
Για να γίνει αυτό, θα μπορούσατε να εφαρμόσετε έναν χρωματικό κωδικό τόσο στα παζλ σας όσο και σας ομάδες των μαθητών σας. Σε κάθε ομάδα θα δοθεί ένα χρώμα και θα πρέπει να εργαστούν σε ένα συγκεκριμένο σύνολο παζλ που έχουν το ίδιο χρώμα με την ομάδα σας. Τα μεταπάζλ – που απαιτούν τη συνεργασία πολλών ομάδων – θα μπορούσαν να έχουν μια ετικέτα με πολλά χρώματα ομάδων. Θα βρείτε ένα παράδειγμα ακολουθίας παζλ χωρισμένο σε ομάδες παρακάτω. Οι πιθανότητες των ακολουθιών παζλ είναι άπειρες.
Ωστόσο, ο χρωματικός κώδικας δεν πρέπει να εμποδίζει τους μαθητές να αλληλοβοηθούνται μεταξύ τους ακόμα και εάν βρίσκονται σε διαφορετικές ομάδες. Επομένως, θα πρέπει να εξηγήσετε ξεκάθαρα στην αρχή ότι θα έχουν το δικαίωμα – και πρέπει – να βοηθήσουν ο ένας τον άλλον, για να τα καταφέρουν στο δεδομένο χρονικό πλαίσιο.
Από όλες τις διαφορετικές δομές, οι πολυγραμμικές διαδρομές ενισχύουν τη συνεργασία και την ομαδικότητα. Με αυτή τη διαδρομή, οι μαθητές θα πρέπει να συζητήσουν τις ανακαλύψεις και τις λύσεις τους, καθώς και τα προβλήματα και δυσκολίες για να τα καταφέρουν.
Με σαφείς οδηγίες και διαφορετικά επίπεδα δυσκολίας, η πολυγραμμική διαδρομή θα ταιριάξει στους περισσότερους μαθητές σας.
Μειονεκτήματα
Από την άλλη πλευρά, το κύριο μειονέκτημα των πολυγραμμικών διαδρομών είναι η πολυπλοκότητά τους στο σχεδιασμό και την κατασκευή. Θα χρειαστούν αρκετές φάσεις δοκιμών και προσαρμογών για την εξάλειψη όλων των δυσλειτουργιών και λαθών από την ακολουθία. Μην περιμένετε να το κάνετε σωστά με την πρώτη προσπάθεια, ειδικά στην αρχή της δημιουργικής διαδικασίας σας. Η επιμονή είναι το κλειδί!
Συμπληρωματικά, η δημιουργία τους θα είναι πιο χρονοβόρα σε σχέση με τις ανοιχτές και τις γραμμικές διαδρομές, καθώς πρέπει να δημιουργηθούν περισσότερα παζλ.
Τέλος, οι αρχάριοι και οι νεαροί μαθητές μπορεί να αισθανθούν χαμένοι και μπερδεμένοι. Όπως αναφέρθηκε παραπάνω, αυτό το πρόβλημα μπορεί να λυθεί χρησιμοποιώντας ένα κωδικό χρώματος, για να κατευθύνει τις ομάδες προς το αίνιγμα που θα πρέπει να λύσουν. Εναλλακτικά, μια σαφής επεξήγηση στην αρχή, σε συνδυασμό με ενδείξεις σε περίπτωση ανάγκης, θα κάνει τη διαδικασία πιο ευχάριστη.
Σημεία που πρέπει να θυμάστε κατά τη δομή της ακολουθίας του παζλ σας
Κατά τη δημιουργία οποιασδήποτε από τις τρεις ακολουθίες πάζλ που αναλύθηκαν σε όλα τα Μαθήματα 13 έως 15, υπάρχουν ορισμένα σημεία που πρέπει να έχετε υπόψη:
- Μπορεί να είναι δελεαστικό να δημιουργήσετε πολλά παζλ. Προσπαθήστε να το αποφύγετε, έχοντας υπόψη τον χρόνο που είναι διαθέσιμος για την επίλυση του δωματίου. Θα εξοικονομήσετε χρόνο. Ο σωστός αριθμός παζλ ανά ακολουθία θα εξαρτηθεί από την τάξη σας, την ηλικία των μαθητών σας, και το επίπεδο δυσκολίας, το οποίο πρέπει να είναι μεταβαλλόμενο. Επομένως, η καλύτερη λύση είναι να πειραματιστείτε.
- Φροντίστε να υποδείξετε ξεκάθαρα τα σημεία έναρξης και λήξης, για να αποφύγετε να χάσετε πάρα πολύ χρόνο με σύγχυση και περιπλάνηση στο δωμάτιο.
- Μπορείτε να μοιράζετε μικρές επιβραβεύσεις κατά τη διάρκεια του παιχνιδιού, για να διατηρείτε το ενδιαφέρον των μαθητών και να τους προσφέρετε μια συνεχή αίσθηση ικανοποίησης (Escape rooms on social entrepreneurship, 2019) – όπως να βρουν ένα στοιχείο ή ένα κρυφό κουμπί που θα ανοίξει μια πόρτα που θα δώσει μια περαιτέρω ένδειξη για το πώς να χρησιμοποιήσουν το αρχικό στοιχείο στην επίλυση του παζλ.
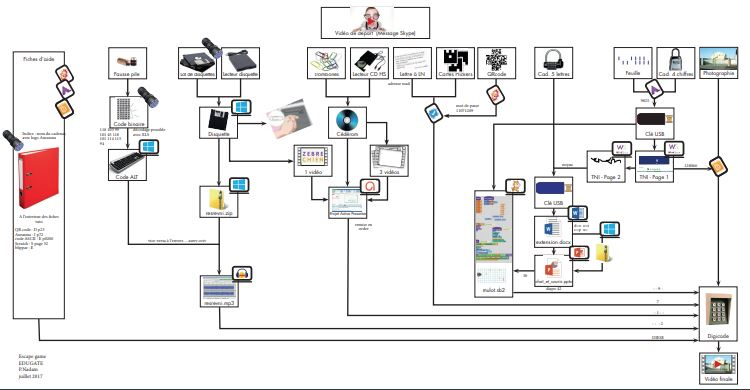
- Δημιουργήστε ένα σχέδιο της δομής του παζλ σας για να οργανωθείτε, ειδικά εάν συμπεριλαμβάνεται μια πολυγραμμική διαδρομή. Παρακάτω θα βρείτε ένα χαρτογραφημένο παράδειγμα. Παρόλο που μπορεί να είναι ελαφρώς υπερβολικό, καθώς ο αριθμός των παζλ είναι σημαντικός, δείχνει πόσο απαραίτητο είναι να χαρτογραφήσετε τη δομής σας εάν αποφασίσετε να δημιουργήσετε μια πολύπλοκη διαδρομή.
Τέλος, η πολυγραμμική διαδρομή ήταν η τελευταία δομή που παρατηρήθηκε από τον Nicholson (2015). Τώρα έχετε όλες τις κάρτες για να δημιουργήσετε την τέλεια ακολουθία παζλ. Στο επόμενο μάθημα θα μάθετε για διαδικτυακά εργαλεία για να προχωρήσετε στη δημιουργία δωματίων διαφυγής.