Στο προηγούμενο μάθημα, κάναμε μια επισκόπηση της βασικής δομής ενός γρίφου δωματίου απόδρασης και ανακαλύψαμε διαφορετικά είδη γρίφων. Σε αυτό το μάθημα καθώς και στα επόμενα, θα δούμε τις διαφορετικές δυνατότητες που υπάρχουν για την οργάνωση μιας αλληλουχίας γρίφων, προκειμένου να δημιουργηθεί ένα λειτουργικό Δωμάτιο Απόδρασης.
Ο Nicholson προτείνει τρία είδη μονοπατιών που θα επεξηγήσουμε σε αυτό και το επόμενο μάθημα.
Πρώτα, ας συζητήσουμε για το γραμμικό μονοπάτι.
Το όνομα του εκφράζει και το περιεχόμενό του. Η οργάνωση των γρίφων ακολουθεί μια γραμμή, μια ακολουθία, ο καθένας από αυτούς ακολουθείται από έναν άλλον. Η επίλυση του πρώτου γρίφου οδηγεί στον δεύτερο, ο δεύτερος στον τρίτο κ.ο.κ. μέχρι και τον τελευταίο γρίφο, ο οποίος ξεκλειδώνει το δωμάτιο. Ο Nicholson (2015) καταγράφει τη χρήση του σε ποσοστό 37% στις εγκαταστάσεις που συμμετείχαν στην έρευνά του.
Απεικόνιση
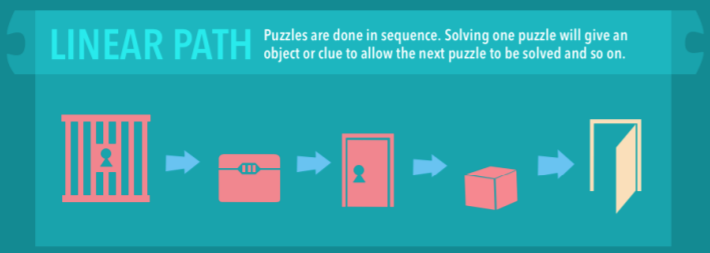
Η παρακάτω γραφική αναπαράσταση των Wiemker κ.α. (2015) μπορεί να σας βοηθήσει να οπτικοποίησετε το τι εννοούμε με τον όρο γραμμικό μονοπάτι.1
Ο πρώτος γρίφος είναι μια ασφαλισμένη πόρτα. Το επιτυχές άνοιγμά της, αποκαλύπτει ένα σεντούκι (γρίφος 2). Μπορούμε να φανταστούμε ότι το σεντούκι εμπεριέχει ένα κλειδί που ανοίγει την πόρτα (γρίφος 3), πίσω από την οποία υπάρχει ένα κουτί (γρίφος 4). Ένας τελευταίος γρίφος οδηγεί στο άνοιγμα του κουτιού, το οποίο εμπεριέχει ένα κλειδί/κωδικό για την απόδραση.
Πλεονεκτήματα
Είναι η απλούστερη και η πιο ξεκάθαρη λύση για την κατασκευή ενός Δωματίου Απόδρασης. Ως καθηγητές που είστε στο ξεκίνημα της δημιουργίας εκπαιδευτικών δωματίων, πιθανότατα να αρχίσετε με αυτό το σχέδιο. Είναι προτιμότερο να το εφαρμόσετε με νεαρούς και αρχάριους συμμετέχοντες για να παρουσιάσετε την αρχή του παιχνιδιού, αποφεύγοντας έτσι τις πολλές πληροφορίες, τις παρεξηγήσεις, και την αποθάρρυνση. Τα γραμμικά μονοπάτια παρέχουν μια σαφή δομή. Οι συμμετέχοντες γνωρίζουν από που να ξεκινήσουν, τι χρειάζεται να κάνουν και που τελειώνει το δωμάτιο.
Ένα επιπλέον όφελος της γραμμικής δομής είναι το γεγονός ότι η ακολουθία του γρίφου είναι προκαθορισμένη. Οι δυνατότητες είναι απεριόριστες, κάτι που επιτρέπει στον σχεδιαστή να εξετάσει την ακολουθία ενδελεχώς από πριν και να αποφύγει δυσλειτουργίες. Δυστυχώς, αυτά τα πλεονεκτήματα συμβαδίζουν με αρκετά μειονεκτήματα που ίσως συναντήσετε στην πορεία σας. Εξαρτάται από εσάς να αποφασίσετε αν επισκιάζουν τα πλεονεκτήματα, βασιζόμενοι στην εμπειρία σας και στην οπτική γωνία των μαθητών.
Μειονεκτήματα
Αρχικά, μειώνει την πιθανότητα της συνεργασίας για την επίλυση. Τα εκπαιδευτικά δωμάτια απόδρασης συχνά απαιτούν ομάδες των 8 με 10 ατόμων, ο οποίος είναι ο υψηλότερος αριθμός παικτών και συναντάται συνήθως σε επαγγελματικές εγκαταστάσεις σε όλο τον κόσμο, οι οποίες στην Ευρώπη εμπλέκουν γύρω στους 4 παίκτες (Nicholson, 2015). Ενώ 4 άτομα πιθανώς να μπορούν να ασχοληθούν μονάχα με έναν γρίφο, η δομή του γραμμικού μονοπατιού δεν θα μπορεί να εξυπηρετήσει 8 άτομα ή περισσότερα. Αυτό σημαίνει ότι, αρκετά συχνά, στο πλαίσιο αυτού του μονοπατιού ενός γρίφου, μερικοί μαθητές θα εξοστρακιστούν λόγω του ότι δεν θα έχουν να ασχοληθούν με κάποιο πρόβλημα, είτε κάτι τέτοιο προκύπτει από τη θέλησή τους είτε όχι. Αυτό έχει ως αποτέλεσμα τη μείωση του αισθήματος της επίτευξης και μπορεί να οδηγήσει σε βαρεμάρα (Δωμάτια Απόδρασης για την Κοινωνική Επιχειρηματικότητα, 2020). Επιπρόσθετα, μπορεί να παρατηρήσετε ότι ένας ή περισσότεροι μαθητές ξεχωρίζουν και ξεκλειδώνουν τους γρίφους χωρίς να ζητάνε βοήθεια από τους συμμαθητές τους (Γραμμικό μονοπάτι έναντι Μη-γραμμικού μονοπατιού, χ.χ.), κάτι που υποβαθμίζει την πιθανότητα συνεργασίας.
Ωστόσο, η συνεργασία και η συνεργασία είναι η ουσία των δωματίων Escape. Οι παίκτες της ομάδας πρέπει να επικοινωνούν, να σκέφτονται συλλογικά, να ανταλλάσσουν και να μοιράζονται (Escape game, 2018). Η προσθήκη ενδείξεων, ιδεών και πληροφοριών μαζί με την ανταλλαγή εργασιών μεταξύ των συμμετεχόντων είναι απαραίτητη για την πρόοδο του παιχνιδιού και την επίλυσή του. Προωθεί τη συλλογική νοημοσύνη. Pierre Levy (2018, όπως αναφέρεται στο Fenaert et al., 2019, p.27, Translated by the author from French «Η συλλογική νοημοσύνη είναι η τέχνη της ταυτόχρονης μεγιστοποίησης της δημιουργικής ελευθερίας και της συνεργατικής αποτελεσματικότητας».) Το περιγράφει ως «η τέχνη ταυτόχρονα μεγιστοποιήστε τη δημιουργική ελευθερία και τη συνεργατική αποτελεσματικότητα ». Μπορεί να παρατηρήσετε κάποιες παραλλαγές στην ποιότητα της συνεργασίας, είτε οι μαθητές των ομάδων γνωρίζουν ο ένας τον άλλον είτε όχι, για προφανείς λόγους.
Επιπρόσθετα, αν οι συμμετέχοντες κολλήσουν σε ένα γρίφο και οι ενδείξεις δεν είναι αρκετά βοηθητικές για την επίλυσή του, είτε το παιχνίδι θα τελειώσει είτε η λύση θα δοθεί από το συντονιστή του παιχνιδιού/εκπαιδευτικό, κάτι που υπονομεύει το σκοπό του παιχνιδιού και της όλης εκπαιδευτικής διαδικασίας. Μπορεί επίσης να οδηγήσει στην απογοήτευση.
Με αυτή τη λογική, σας συνιστούμε να εφαρμόσετε το γραμμικό μονοπάτι στο ξεκίνημα της δημιουργικής σας πορείας αλλά σταδιακά να απομακρυνθείτε από αυτό, όσο κερδίζετε αυτοπεποίθηση. Ίσως συναντήσετε αυτά τα μειονεκτήματα ενώ δοκιμάζετε το σενάριό σας με τους μαθητές. Προσπαθήστε να θεωρήσετε αυτά τα μειονεκτήματα ως έναυσμα για βελτίωση. Χρησιμοποιήστε τα έτσι ώστε η επόμενη ακολουθία γρίφων να είναι καλύτερη.
Αφού εξετάσαμε τη δομή, τα πλεονεκτήματα και τα μειονεκτήματα του γραμμικού μονοπατιού, θα αναφερθούμε λεπτομερώς σε περισσότερα μονοπάτια στα μαθήματα 14 και 15. Αυτό θα σας προσφέρει περισσότερες λύσεις προς αποφυγήν των προβλημάτων που παρουσιάστηκαν παραπάνω και για τη δημιουργία ακολουθίας γρίφων, πάνω στην οποία θα μπορούν να συνεργαστούν όλοι οι μαθητές.