Στο προηγούμενο μάθημα, αναφερθήκαμε στα πλεονεκτήματα και τα μειονεκτήματα της δημιουργίας παζλ για τα δωμάτια διαφυγής σας, τα οποία ακολουθούν μια γραμμική διαδρομή. Σε αυτό το μάθημα, θα παρουσιάσουμε τη δεύτερη διαδρομή που περιγράφεται από τον Nicholson (2015): την ανοιχτή διαδρομή.
Η ανοιχτή διαδρομή αποτελείται από παζλ που μπορούν να λυθούν με οποιαδήποτε σειρά (Wiemker et al., 2015). Όλα τα παζλ, εκτός από το τελευταίο, είναι διαθέσιμα για αλληλεπίδραση από την αρχή του παιχνιδιού. Κάθε παίκτης μπορεί να επιλέξει σε ποιο να επικεντρωθεί, έχει τη δυνατότητα να αλλάξει και να επιστρέψει σε αυτό σε μεταγενέστερο στάδιο. Το τελευταίο παζλ – που συχνά ονομάζεται μεταπάζλ (metapuzzle) – είναι συνήθως μπλοκαρισμένο και οι παίκτες δεν μπορούν να το επεξεργαστούν έως ότου ολοκληρώσουν τα υπόλοιπα παζλ. Τα στοιχεία για την επίλυσή του προέρχονται συνήθως από τις προηγούμενες απαντήσεις που έχουν προκύψει (Wiemker et al., 2015). Η λύση κάθε αρχικού παζλ περιέχει μέρη ενός νέου αινίγματος που πρέπει να συνδυαστούν για να επιλυθεί το μεταπάζλ.
Παράδειγμα με εικόνα
Το ακόλουθο ενημερωτικό γράφημα από τον Wiemker et al. (2015) μπορεί να σας βοηθήσει να σχηματίσετε μία εικόνα για το τί σημαίνει η ανοιχτή διαδρομή.
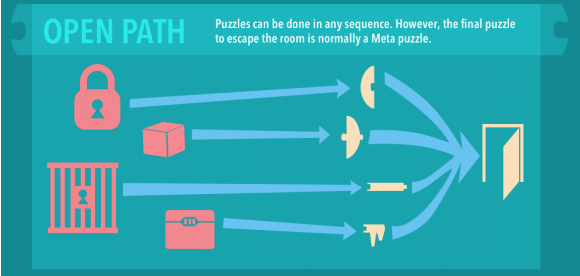
Από την αρχή, έχουμε 4 διαφορετικά παζλ: μια κλειδαριά, ένα κουτί, μια πύλη και ένα σεντούκι. Όλα αυτά πρέπει να ανοιχθούν την κατάλληλη στιγμή και ξεχωριστά. Απαιτείται ένα αίνιγμα για καθένα από αυτά. Κάθε ένα από αυτά συνήθως περιέχει ένα νέο παζλ ή ένα μέρος της λύσης για το μεταπάζλ – στο παράδειγμα είναι τα μέρη ενός κλειδιού – τα οποία πρέπει να συνδυαστούν για να ανοίξει η πόρτα της εξόδου.
Στη συνέχεια, βλέπουμε δύο παραδείγματα μεταπάζλ που θα μπορούσαν να χρησιμοποιηθούν στο STEM:
- Στα Μαθηματικά, μπορούμε να φανταστούμε μέρη μιας εξίσωσης που θα πρέπει να συνδυαστούν και στη συνέχεια να λυθούν για να ανοίξει μια κλειδαριά πάνω στην πόρτα εξόδου.
- Στη Χημεία, μπορούμε να φανταστούμε ένα κομμένο μόριο που θα πρέπει να ανασυσταθεί. Ο χημικός τύπος θα μπορούσε να είναι ο κωδικός για το άνοιγμα ενός κρυπτόλεξου που περιέχει το κλειδί για την πόρτα (π.χ. NaCl για χλωριούχο νάτριο ή C6H12O6 για γλυκόζη).
Το κρυπτόλεξο είναι ένα φορητό θησαυροφυλάκιο που εμφανίστηκε για πρώτη φορά το 2003 στον Κώδικα Ντα Βίντσι του Νταν Μπράουν (Cryptex, 2019). Είναι πιο εύκολο να το λύσετε απ’ ότι φαίνεται. Μπορείτε να το φτιάξετε στο σπίτι με χαρτόνια και χαρτί, αρκεί να έχετε αρκετό χρόνο (Nadam, 2019). Επίσης μπορείτε να αγοράσετε από το Διαδίκτυο πλαστικά κρυπτόλεξα του εμπορίου και το μόνο που θα σας ζητηθεί είναι να το ρυθμίσετε.

Πλεονεκτήματα
Αυτή η διαδρομή δεν είναι η πιο διαδεδομένη στον κόσμο. Ο Nicholson (2015) την εντόπισε μόνο στο 13% των 175 εγκαταστάσεων που ερεύνησε. Ωστόσο, προσαρμόζεται περισσότερο σε εκπαιδευτικά δωμάτια διαφυγής απ’ ότι οι γραμμικές διαδρομές. Όπως αναφέραμε προηγουμένως, στα εκπαιδευτικά δωμάτια διαφυγής συμμετέχουν συνήθως έως και 10 μαθητές ανά παιχνίδι, όπου είναι ένας υψηλός αριθμός για να αποδειχθεί αποτελεσματική η γραμμική δομή. Αντίθετα, η ανοιχτή διαδρομή επιτρέπει την ταυτόχρονη συμμετοχή περισσότερων ανθρώπων στη διαδικασία επίλυσης. Στο παραπάνω παράδειγμα του Wiemker’s et al., δύο μαθητές θα μπορούσαν να προσπαθήσουν να λύσουν το παζλ που σχετίζεται με την κλειδαριά, ενώ τρεις άλλοι θα μπορούσαν να προσπαθήσουν να ανοίξουν το σεντούκι και ούτω καθεξής.
Πρώτον, θα ενισχύσει τη συνεργασία
- μέσα σε μικρές ομάδες που εργάζονται στα αρχικά παζλ
- που απαιτείται μεταξύ μικρών ομάδων για την επίλυση του τελικού παζλ. Οι παίκτες θα πρέπει να μοιραστούν τις ιδέες τους, τις ανακαλύψεις τους και να εξηγήσουν τη διαδικασία σκέψης τους.
Επιπλέον, εάν μια ομάδα τελειώσει το παζλ της πριν από την άλλη, οι μαθητές της πρώτης ομάδας θα μπορούσαν να βοηθήσουν τους συμμαθητές τους να λύσουν το παζλ τους. Εάν δύο ομάδες έχουν κολλήσει, ακόμη και αφού έχουν πάρει συμβουλές, θα μπορούσαν να ανταλλάξουν τα παζλ και να δώσουν μια νέα προοπτική.
Επιπλέον, η ανοιχτή δομή εξακολουθεί να προσφέρει το πλεονέκτημα ότι είναι εύκολη προς εφαρμογή. Σε ορισμένες περιπτώσεις, μπορεί να είναι ακόμη πιο εύκολη από τη δομή γραμμικής διαδρομής, καθώς δεν απαιτείται προβληματισμός σχετικά με την αλληλουχία του παζλ.
Μειονεκτήματα
Το πρώτο πρόβλημα αφορά τη δυσκολία.
Πρώτον, η ανοιχτή διαδρομή θα είναι πιο δύσκολη για άπειρους παίκτες να τη χειριστούν, καθώς αυτή η δομή παζλ υστερεί σε σαφή σημείο εισόδου, καθώς και σε ορατή ακολουθία και λογική. Επίσης μπορεί να δημιουργήσει σύγχυση μεταξύ των μαθητών σας, ειδικά των πιο νεαρών. Ωστόσο, αυτό το πρόβλημα μπορεί να λυθεί με μια σαφή εξήγηση από τον αρχηγό / εκπαιδευτή του παιχνιδιού πριν από την έναρξη του παιχνιδιού, ή με κάποιες ενδείξεις, που μπορούν να δοθούν είτε στην αρχή είτε σε περίπτωση που οι μαθητές κολλήσουν σε κάποιο σημείο για αρκετά λεπτά.
Δεύτερον, οι ανοιχτές διαδρομές υπάρχει περίπτωση να φαίνονται πολύ εύκολες και χωρίς ενδιαφέρον για μαθητές που έχουν ήδη παίξει σε δωμάτια διαφυγής επαγγελματικών εγκαταστάσεων. Οι ανοιχτές διαδρομές μειώνουν την πιθανότητα εκπλήξεων, καθώς όλα είναι διαθέσιμα από την αρχή. Οι έμπειροι παίκτες θα ξέρουν τι να κάνουν. Ωστόσο, η αβεβαιότητα και η ανακάλυψη είναι δύο βασικές μεταβλητές των δωματίων διαφυγής. Η μη διαδοχική σειρά των παζλ θα μπορούσε επομένως να μειώσει την αίσθηση της ολοκλήρωσης και να δημιουργήσει πλήξη.
Δεύτερον, οι ανοιχτές διαδρομές υπάρχει περίπτωση να φαίνονται πολύ εύκολες και χωρίς ενδιαφέρον για μαθητές που έχουν ήδη παίξει σε δωμάτια διαφυγής επαγγελματικών εγκαταστάσεων. Οι ανοιχτές διαδρομές μειώνουν την πιθανότητα εκπλήξεων, καθώς όλα είναι διαθέσιμα από την αρχή. Οι έμπειροι παίκτες θα ξέρουν τι να κάνουν. Ωστόσο, η αβεβαιότητα και η ανακάλυψη είναι δύο βασικές μεταβλητές των δωματίων διαφυγής. Η μη διαδοχική σειρά των παζλ θα μπορούσε επομένως να μειώσει την αίσθηση της ολοκλήρωσης και να δημιουργήσει πλήξη.
Λαμβάνοντας υπόψη αυτό το πλαίσιο, σας συμβουλεύουμε να χρησιμοποιήσετε την ανοιχτή διαδρομή στη μέση της δημιουργικής πορείας σας, αφού δοκιμάσετε τη γραμμική διαδρομή. Εάν ταιριάζει στις ανάγκες σας και στις ανάγκες των μαθητών σας, συνεχίστε. Εάν όχι, απομακρυνθείτε σταδιακά από αυτήν.
Θα περιγράψουμε λεπτομερώς μια επιπλέον διαδρομή στο Μάθημα 15. Θα σας δοθεί μια νέα λύση – πιο δύσκολη, αλλά πιο ελκυστική – για να αποφύγετε τα προβλήματα που αναφέρονται παραπάνω και να δημιουργήσετε μια σύνθετη ακολουθία από παζλ.